例題集 / 情報 / 音声情報処理 / 音声の分析
絞り込み
難易度
フーリエ変換例１
理解レベル
難易度: ★
以下のスペクトル密度関数F(ω)を逆フーリエ変換し、時間関数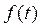
を求めよ。[2-15参照]
 |
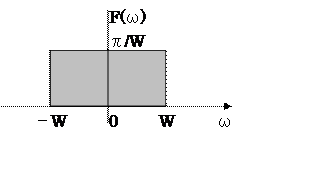解答例・解説
$f(t)=\frac{sin(Wt)}{Wt}=Sa(Wt)$
フーリエ変換例２
理解レベル
難易度: ★
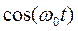のフーリエ変換が 
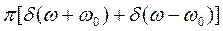となることを示せ。ただし、インパルス関数
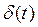を次式のように定義する。[2-15参照]
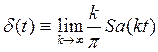なお，
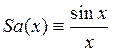である。[2-10参照]
解答例・解説
このフーリエ変換を求めるには，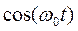
が区間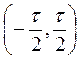
に存在し，この区間以外ではゼロとし，極限で
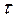を無限大にすればよい。[2-11参照]
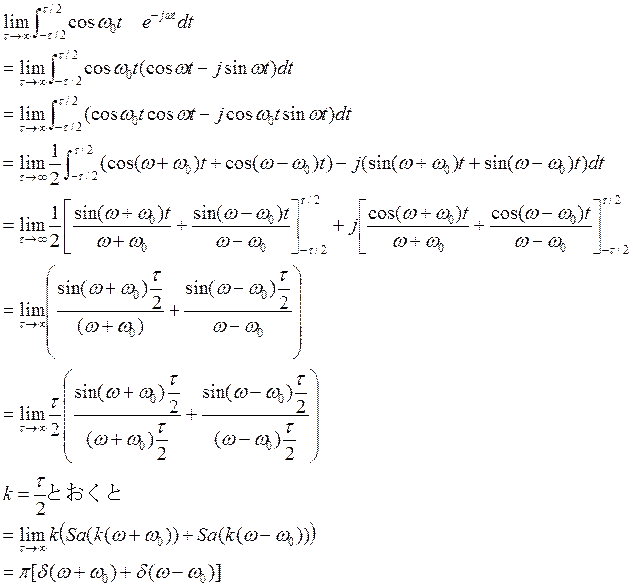
フーリエ変換例 ３
理解レベル
難易度: ★
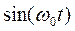のフーリエ変換は
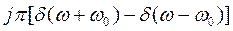となる。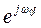
のフーリエ変換を求めよ。[2-11] [2-15⑫参照]
解答例・解説
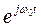F [
]=F [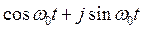
]
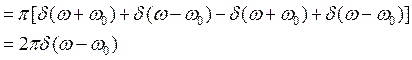
フーリエ変換例 ４
知識・記憶レベル
難易度: ★
周期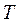
をもつ周期関数
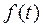の複素フーリエ係数を
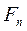とすると，
，
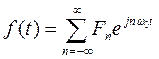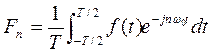
ただし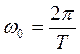
となる。この関係を用いて,周期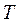をもつ周期関数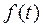のフーリエ変換を求めよ。なお，複素フーリエ係数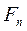はわかっているものとする。
解答例・解説
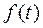F[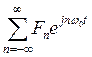
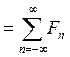]=F[
]
F[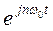
]
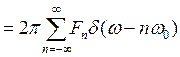[2-12, 2-13参照]
フーリエ変換例 5
理解レベル
難易度: ★
（５）時間関数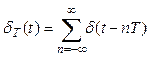
は，周期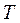
をもつ周期関数である。
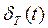の複素フーリエ係数
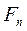を求めよ。
解答例・解説
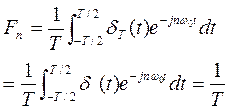[2-16⑯参照]
フーリエ変換例 6
理解レベル
難易度: ★
デルタ関数列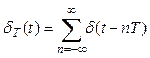 
のフーリエ変換を求めよ。
解答例・解説
F [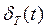
]
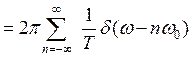
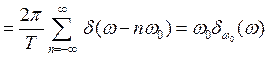[2-16⑯参照]
標本化定理の証明
知識・記憶レベル
難易度: ★
標本化定理を証明せよ。
解答例・解説
%=image:/media/2016/04/21/146122812370137300.png: