音声分析

スペクトル

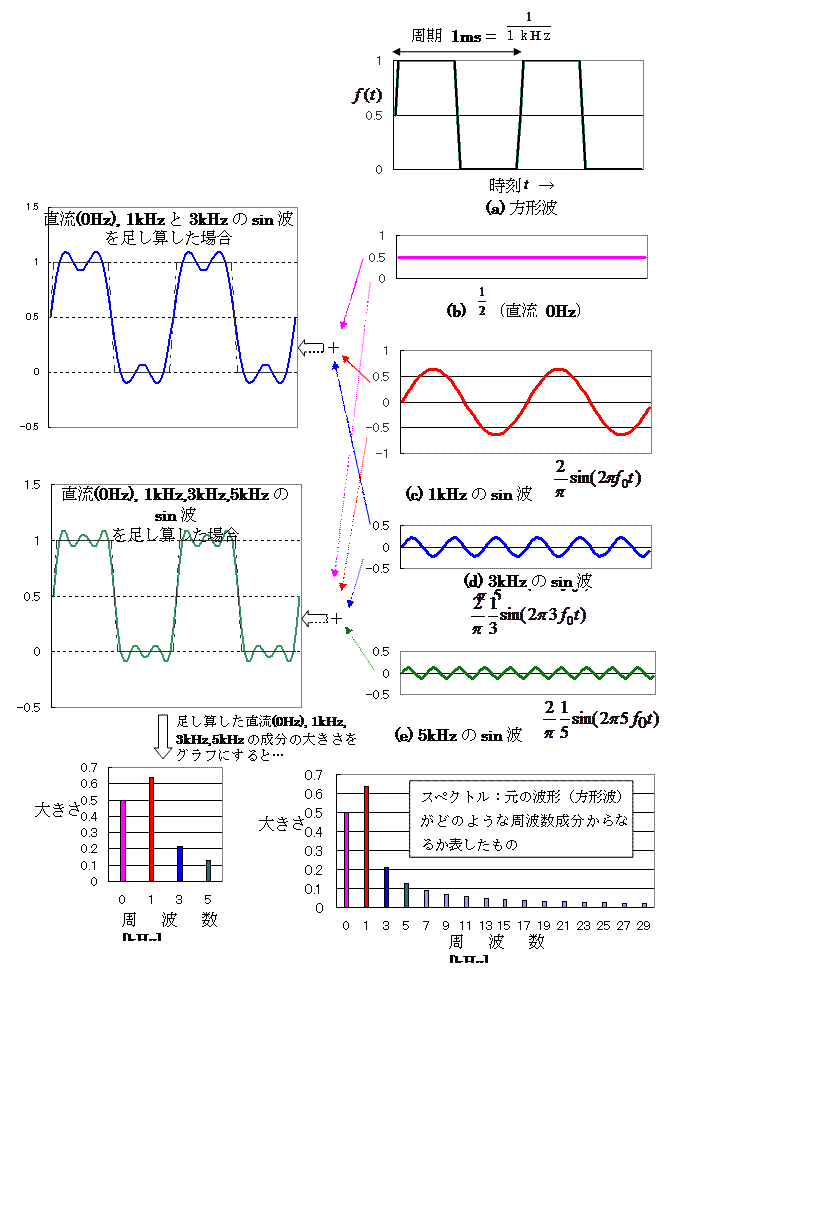
図(a)は、1kHzの方形波である。

この方形波は、(b)~(e)の波形の和で

近似できる。

サンプリング定理（標本化定理）

周波数Hz以上のスペクトル成分をもたない帯域制限信号は、秒以下の等間隔の標本で一義的に決定できる。

フーリエ変換

（１）2πを周期とする関数のフーリエ級数

（２）2Tを周期とする関数のフーリエ級数

（３）2πを周期とする関数の複素フーリエ級数

を周期とする関数の複素フーリエ級数はオイラーの公式を用いて、（１）のフーリエ級数を変形することで、以下のように与えられる。

（４）2Tを周期とする関数の複素フーリエ級数

（５）フーリエ変換の導出

を周期とする関数の複素フーリエ級数において、として整理すると、フーリエ変換が得られる。

      [2-14参照]

, , を、それぞれ時間関数,,のフーリエ変換とする。

（１）時間移動                        [2-18,2-19参照]

（２）周波数移動                       [2-18参照]

（３）時間たたみこみ                 [2-20参照]

（４）周波数たたみこみ          [2-20,2-21参照]

（５）                                                          [2-22参照]

（６）三角形の関数とデルタ間数列の畳み込み概略図                        [2-22参照]